USAHA DAN ENERGI

A. Usaha

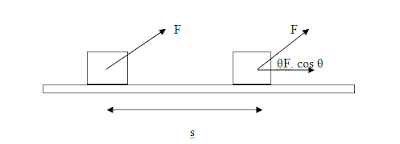
Usaha adalah besarnya gaya yang bekerja pada suatu benda sehingga benda tersebut mengalami perpindahan.

Rumus vektor polar

W = F.s.cos θ

Keterangan :

W        : Usaha (Joule)

F          : Gaya (Newton)

S          : Perpindahan (meter)

θ          : Sudut antara gaya (F) dan vektor perpindahan (s)

Apabila W positif, disebut usaha positif artinya arah gaya searah dengan perpindahan benda.

Apabila W negatif, disebut usaha negatif artinya arah gaya berlawanan dengan perpindahan benda.

Apabila W nol (0), disebut usaha nol artinya perpindahan tidak melakukan usaha pada benda.

Contoh Soal :

Massa benda 2 kg, perpindahan yang dialami benda 3 m.

Berapakah usaha yang terjadi?

Jawab:

W = F.s.cos θ

W = 100.3.cos 60º

W = 100.3.0,5

w = 150 Newton

Rumus Vektor Satuan

W = F.r

Keterangan :

F = ai + bj

R = ei + dj

Contoh Soal :

Sebuah resultan gaya tetap yang dinyatakan dalam vektor satuan F = 4i + 2j bekerja pada sebuah benda hingga mengalami perpindahan r = 5i + j

Berapakah usaha yang terjadi?

Jawab:

W = F.r 

W = (4i + 2j) . (5i + j)

W = (4)(5) + (2)(1)

W = 22 Joule

B. Gaya Konservatif

Gaya Konservatif adalah gaya yang tidak bergantung kepada lintasan dan nilainya selalu tetap.

Contoh gaya konservatif :

Gaya gravitasi F_kons = m.g

Gaya gravitasi Newton F_{grav = G.M.m/}r²

Gaya pegas F_p = k.x

Gaya listrik

Contoh gaya non-konservatif

Gaya gesek

Gaya magnet

C. Hubungan Usaha dan Energi

1. Memindahkan Benda Vertikal 

 W = Ep₂ – Ep₁

_{W =}  m₂ . g₂ . h₂ – m₁ . g₁ . h₁

_{Contoh Soal :}

Sebuah bola bermassa 0,5 kg dilempar vertikal ke atas hingga mencapai ketinggian 11 m. Berapakah perubahan enrgi potensial (usaha) ketika bola berada pada ketinggian 3,5 m?

Jawab :

Energi potensial benda pada ketinggian 11 m

Ep = m . g . h = 0,5 . 10 . 11 = 55 Joule

Energi potensial pada ketinggian 3,5 m

Ep = m . g . h = 0,5 . 10. 3,5 = 17,5 Joule

W = Ep₂ – Ep₁

W = 17,5 – 55 = -37,5 Joule 

_{2. Memindahkan Benda Horizontal}

W = Ek₂ – Ek₁

W =  ½ . m₂ . v₂²  - ½ . m₁ . v₁²

Contoh Soal :

Peluru P (massa = 50 gr) ditembakkan pada balok B (massa = 9,95 kg) yang diam pada bidang mendatar kasar (koefisien kinetis = 0,2) Kecepatan peluru 200 ^m/_s. Hitung jarak tempuh maksimum balok bila peluru menembus bola dengan kecepatan 10 ^m/_s

Jawab :

m₁v₁ + m₂v₂ = m₁v₁’ + m₂v₂’

0,05 . 200 + 9,95 . 0 = 0,05 . 10 + 9,95 . v2’

10 + 0 = 0,5 + 9,95 . v₂’

9,95 = 9,95 . v₂’

v₂’ = 1 ^m/_s

_{W =} Ek₂ – Ek₁

Fg . s = ½ . m₂ . v₂²  - ½ . m₁ . v₁²

(N . µs) . s = ½ . 10 . 0 - ½  . 10 . 1

(100 . 0,2) . s = -5

S = 20 / -5

s = -0,25 m

3. Memindahkan Benda Sembarang

a. Tanpa gaya gesekan (W = 0)

EM₁ = EM₂

Ep₁ + Ek₁ = Ep₂+ Ek₂

_{Contoh Soal :} 

_{Sebuah benda bermassa 2 kg dilemparkan vertikal ke atas dengan kecepatan awal 30 m/s. Bila g = 10} m/s² Berapakah besarnya energi kinetik saat ketinggian benda mencapai 25 m?

_{Jawab :}

Ep₂+ Ek₂ =  Ep₁ + Ek₁ 

m₂ . g₂ . h₂ +  Ek₂  = m₁ . g₁ . h₁  + ½ . m₁ . v₁²

Ek₂ = m(½ . v₁² – gh)

Ek₂ = 2 (½ . 30 . 30 – 10 . 25)

Ek₂ = 400 Joule

b. Ada gaya gesekan

W = EM₂ – EM₁

_{Contoh Soal :} 

Sebuah koper bermassa m = 20 kg ditarik dengan gaya konstan F = 150 N sepanjang suatu lerengan (bidang miring) bandara, dengan kemiringan α = 30° terhadap horizontal sampai mencapai ketinggian 5 m. Tentukan besar gaya gesekan jika kelajuan koper bertambah dari 0 pada dasar bidang menjadi 1 m/s pada ketinggian h.

Jawab:

sin α = 5 / panjang lintasan

Panjang lintasan = 5 / sin α

Panjang lintasan = 5 / 0,5

Panjang lintasan = 10 m

W = EM₂ – EM₁ 

(F . s) - (Fg . s) = (Ep₂+ Ek₂) - (Ep₁ + Ek₁)

(150 . 10) - (Fg . 10) = (20 . 10 . 5 + (½ . 20 . 1) - (20 . 10 . 0 + ½ . 20 . 0)

1500 - 10Fg = 1000 + 10

10 Fg = 490

Fg = 49 Newton 

percobaan

Laporan Pembuatan Roket

1. Tujuan :

"Aplikasi Hukum Kekelan Momentun (HKM) pada prinsip roket"

2. Bahan :

-Sprite

-Botol redoxon beserta tutupnya

-Redoxon

-Kertas Karton

-Lem

-Gunting

3. Prinsip Kerja :

Sistem Lontar : Roket terlempar oleh ledakan bahan kimia berupa cairan sprite pada botol lain 

4. Cara Pembuatan Roket :

   
a. Menyiapkan alat dan bahan yang dibutuhkan untuk membuat roket.

b. Memulai membuat roket dengan kertas karton dari kerucutnya, badan roket, dan sayap roket.

c. Setelah itu, mengisi botol redoxon dengan 2 butir redoxon dan sprite sebanyak ½ botol lalu menutup botol redoxon dengan tutupnya dan meletakkan roket.
d. Mengocok/menggoyangkan botol redoxon lalu membaliknya dan mendiamkannya sekitar beberapa detik. 

e. Badan botol redoxon akan terlempar ke atas.

5. Hasil :

      a. Foto Roket

      b. Video Roket Terbang   

http://www.youtube.com/watch?v=IcqctutILKA&feature=youtu.be

      c. Bagan roket

FUNGSI VEKTOR

tugas fisika

CYNTHIA MONICA XI IPA 2-3
AMELIA SIDHARTA XI IPA 2-6
DIONISIUS XI IPA 2-10
INDRA REVATA H. XI IP1 2-24

Implementasi Vektor Satuan Dalam Kehidupan Sehari – Hari

Latar belakang :

Bicara tentang fungsi vektor, ada baiknya jika kita tahu terlebih dahulu apa itu vektor. Dalam fisika kita mengenal vektor sebagai sebuah besaran yang memiliki nilai dan arah. Sedangkan dalam matematika, vektor adalah anggota dari ruang vektor. Secara geometris, vektor dapat disajikan dengan ruas garis berarah. Panjang ruas garis menyatakan besar vektor dan anak panah menyatakan arah vektor.

Pada dasarnya, setiap bagian dari matematika memiliki fungsi masing-masing. Baik fungsi matematisnya, penerapannya dalam kehidupan maupun kaitannya dengan ilmu agama. Tidak terkecuali dengan vektor.

Kadang kala, muncul sebuah pertanyaan dari kalangan peserta didik, dimana mereka menanyakan apa tujuannya, atau apa pentingnya kita mempelajari perihal bidang pembelajaran seperti ini? Vektor, Fungsi vektor, turunan fungsi vektor, bukankah dalam kehidupan sehari-hari kita tidak akan ditanyai orang-orang tentang apa itu vektor? Atau mereka tidak akan bertanya, berapa hasil dari turunan vektor berikut ini. terdengar lucu memang, namun akan lebih baik jika kita bisa menjelaskan sedikit bagaimana aplikasi dari vektor ini dalam kehidupan manusia. Sehingga mempelajarinya bukanlah sebuah kesia-siaan.

Rumusan Masalah :

Bagaimanakah fungsi vektor

Tujuan dan Manfaat Penulisan :

Mengetahui fungsi dan penerapan vektor satuan dalam kehidupan sehari – hari

Tinjauan pustaka :

Penerapan fungsi vektor posisi dalam kehidupan, yaitu :

1.      Sarana transportasi darat, laut, maupun udara masing-masing memiliki peluang yang sama untuk terjadinya kecelakaan. Apabila kecelakaan teradi di tengah lautan lepas tentunya kapal yang mengalami kerusakan hars dibawa ke pelabuhan terdekat untuk segera diperbaiki. Untuk menarik kapal tersebut dibutuhkan dua buah kapal dengan dilengkapi kawat baja. Agar kapal dapat sampai ke pelabuhan yan dituju dan posisi kapal selama perjalanan tetap stabil besar gaya yang dibutuhkan oleh masing-masing kapal penarik dan sudut yang di bentuk oleh kawat baja harus diperhitungkan dengan cermat.

2.      Dalam Navigasi, vektor berpengaruh besar terhadap keberadaan suatu lokasi ditinjau dari tempat yang bergerak (kendaraan atau lainnya). Teknologi ini disebutGlobal Positioning System atau GPS. Dimana sistem ini memberitahukan lokasi di permukaan bumi walaupun tempatnya bergerak. Sehingga, suatu kendaraan dapat tahu keberadaannya dan dimana lokasi tujuannya. Karena itu vektor sangat berperan penting dalam Navigasi contohnya vector yang digunakan untuk Sistem Navigasi Pesawat Terbang. Semua pesawat terbang dilengkapi dengan sistem navigasi agar pesawat tidak tersesat dalam melakukan penerbangan. Panel-panel instrument navigasi pada kokpit pesawat memberikan berbagai informasi untuk sistem navigasi mulai dari informasi tentang arah dan ketinggian pesawat. Pengecekan terhadap instrument sistem navigasi harus seteliti dan seketat mungkin. Sebagai contoh kejadian yang menimpa pesawat Adam Air pada bulan pebruari 2006 sewaktu menjalani penerbangan dari bandara Soekarno Hatta menuju bandara Hasanudin di Makasar. Ketidaktelitian pihak otoritas penerbangan yang mengijinkan pesawat Adam Air terbang dengan sistem navigasi yang tidak berfungsi menyebabkan Pesawat Adam Air berputar-putar di udara tanpa tahu arah selama tiga jam, sebelum mendarat darurat di bandara El Tari Nusa Tenggara Timur. Kesalahan akibat tidak berfungsinya system navigasi adalah kesalahan yang fatal dalam dunia penerbangan. Sanksi yang diberikan adalah dicabutnya ijin operasi bagi maskapai penerbangan yang melanggar. Vektor menyatakan arah dan besar suatu besaran. Jurusan tiga angka, Analisi ruang, Navigasi penerbangan dan pelayaran selalu menggunakan vektor untuk keperluan itu. Peralatan navigasi membutuhkan perhitungan vektoris yang sudah dikalibrasikan dengan alat ukur sehingga menghasilkan keluaran manual atau digital. Keluaran itu dapat dibaca pada pada alat ukur yang menera besar dan arah secara bersamaan, sehingga bermanfaat bagi orang yang memantaunya.

3.      Pernahkah Kamu naik pesawat terbang? Antara penumpang dan pilot dan copilot di ruang kemudi dipisah dengan sekat. Tujuannya agar pilot dapat berkonsentrasi mengemudikan pesawat. Pernahkah Kamu bayangkan pesawat terbang di malam hari? Bagaimana pilot mengemudikan pesawat terbang di malam hari. Dengan sistem vektor yang dikalibrasikan dengan komputer navigasi pesawat pilot dapat memantau arah tujuan pendaratan pesawat. Jadi tidak pernah sebuah pesawat nyasar ke lain tempat.

4.      Dalam sains komputer vektor digunakan untuk pembuatan gravis. Grafis adalah gambar yang tersusun dari koordinat-koordinat. Dengan demikian sumber gambar yang muncul pada layar monitor komputer terdiri atas titik-titik yang mempunyai nilai koordinat. Layar Monitor berfungsi sebgai sumbu koordinat x dan y. Grafis vektor adalah objek gambar yang dibentuk melalui kombinasi titik-titik dan garis dengan menggunakan rumusan matematika tertentu. Contoh software yang menggunakan vektor adalah CorelDRAW dan Adobe Illustrator. Dalam software komputer seperti AutoCAD, Google SketchUp dll, terdapat penghitungan vektor yang terkomputerisasi. Program tersebut berfungsi sebagai penggambar rancangan bangunan 3D sebelum membangun bangunan sebenarnya. Dalam progeam tersebut terdapat tiga sumbu, sumbu X, sumbu Y dan sumbu Tegak (3 dimensional).

5.      Ketika penerjun menjatuhkan diri dari kapal, tempat ia jatuh tidak tepat di bawah kapal, tetapi jauh melenceng karena adanya dua vektor gaya yaitu gaya gravitasi dan gaya dorong angin.

6.      Saat perahu menyebrangi sungai, makan kecepatan perahu yang sebenarnya merupakan kecepatan gerak perahu dan kecepatan air.

7.      Dalam suatu kejadian seorang pemanah menarik anak panah dari busurnya, sebenarnya arah gerak anak panah merupakan penjumlahan vektor gaya tarik tali dari kedua unjung busur tersebut.

8.      Metode vektor juga diaplikasikan terhadap seseorang yang sedang bermain layang-layang. Sehingga arah layang-layang yang sedang terbang tidak lurus terhadap orang yang memegang tali layangan. Dengan demikian orang tersebut dapat melihat layangan  lebih jelas karena ada pengaruh vektor.

9.      Pada saat seorang anak bermain jungkat-jungkit, pada bidang miring menggunakan gaya vektor, sehingga anal tersebut tidak jatuh dari bidang miring itu.

10.  Seorang pilot pada pesawat terbang menggunakan komputer navigasi.

Kesimpulan :

Vektor posisi digunakan sebagian besar untuk keperluan navigasi dalam kehidupan.

Daftar Pustaka/Referensi :

1.      R.Spiegel,Murray.1991.AnalisisVektor.Jakarta: Erlangga

2.      http://elearning.gunadarma.ac.id/docmodul/matematika_lanjut/bab7-fungsi_vektor.pdf (23-06-2013/19:43)

3.      http://metricmatik.blogspot.com/2011/04/makalah-kegunaan-kalkulus-vektor.html(24-06-2013/02:53)

4.      http://caemaqo.blogspot.com/ (24-06-2013/02:53)

5.      http://simplemomentum.blogspot.com/2012/05/penerapan-vektor-dalam-kehidupan-sehari.html (24-06-2013/01:34)